2.2. Técnicas de ModeladoExisten multitud de técnicas de modelado 3D. En una primera taxonomía de alto nivel podemos hacer una categorización dependiendo de si el modelado se centra en definir únicamente las características del contorno del objeto:
Debido a las posibilidades de tratamiento, operadores y velocidad de procesamiento, la mayoría de los paquetes de diseño gráfico permiten el modelado de contorno. Dentro de esta categoría distinguimos entre modelado poligonal y modelado mediante curvas (ver Figura 01).  Figura 01. Superficie definida mediante curvas NURBS y mediante polígonos. Modelado Poligonal Vs. Modelado mediante CurvasLos modelos poligonales son ampliamente utilizados, debido a su velocidad de procesamiento y a la exactitud de definición que permite. Hay que tener en cuenta el fin para el que se construirá el modelo para decidir el nivel de detalle con el que se definirá su geometría. No es lo mismo construir un modelo para un videojuego, donde el número de polígonos es crítico debido a que debe ser representado de forma interactiva a un alto número de frames por segundo, que un modelo que se destinará a una película de animación. Otros factores tales como distancia con la cámara virtual o importancia del modelo en la escena condicionarán el nivel de detalle de la geometría que forma el modelo. El hardware de las tarjetas aceleradoras 3D está preparado para trabajar óptimamente con triángulos. Sin embargo, la definición de una superficie curva con un alto nivel de detalle puede requerir un altísimo número de polígonos. Por ello, en ciertas ocasiones puede ser interesante utilizar directamente superficies curvas. Frente a la representación basada en conjuntos de polígonos, las curvas pueden ser descritas de un modo preciso mediante una ecuación. Estas ecuaciones, como veremos, pueden ser evaluadas y convertidas a conjuntos de polígonos (típicamente triángulos) en el momento de su representación (Rendering). Entre las características que hacen el modelado mediante curvas interesante, se puede destacar:  Figura 02. Modos de sombreado.
Desde el punto del vista del diseñador, una de las principales ventajas de los modelos poligonales es el alto número de operadores de modelado existentes. Esta es una de las razones por las que el modelado mediante superficies curvas se emplea Sombreado de SuperficiesEl uso de mallas poligonales simplifica la escritura de ciertas partes del software de diseño 3D, como el motor de render. En general los triángulos aproximan una superficie compleja que es la que queremos definir cuando modelamos. No es posible usar los "infinitos" triángulos que harían falta para definir correctamente algunas superficies, de modo que hay que recurrir a algunos trucos de sombreado para ocultarlos. Hay dos formas de presentar una superficie de triángulos en el render. Una de ellas es asumir que el objeto es localmente plano. Es decir, que no tiene curvatura alguna, sólo una serie de caras planas. Es el caso de un cubo, que tiene 6 caras cuadradas y por lo tanto 12 triángulos como mínimo para definirlo. Al renderizarlo se asume que los triángulos son planos y de normal constante. En la Figura 02 vemos como el sombreado cambia bruscamente entre cada par de caras de la calavera superior. Esto es debido al cambio del vector normal entre triángulos. Sin embargo hay otros casos en los que se pretende simular una superficie curva y suave como una esfera. En estos casos no nos podemos permitir un salto brusco de normal de un triángulo a otro; se puede indicar a Blender que suavice los vectores normales de las caras. Para esto se asigna una normal a cada vértice de la superficie. Generalmente basándose en la media de las normales de las caras que delimitan con el vértice en cuestión. Después, a la hora de renderizar, se interpola la normal entre los vértices del triángulo, por lo que deja de ser una normal constante. En el borde entre dos triángulos las normales son iguales a ambos lados, por lo que con una definición aceptable el ojo no detectará la presencia de triángulos en la superficie. Los objetos de la Figura 02 tienen idéntica geometría. La diferencia es que el objeto superior no tiene las normales suavizadas mientras que el inferior sí. En la calavera no suavizada se pueden apreciar claramente las caras poligonales. En algunas zonas, como en la zona entre los ojos, vemos cuadrados en lugar de triángulos debido a que están alineados formando facetas de cuatro vértices.
No obstante, no conviene abusar del suavizado en exceso. Esto quiere decir que no debemos intentar simular superficies suaves usando muy pocas caras dado que:
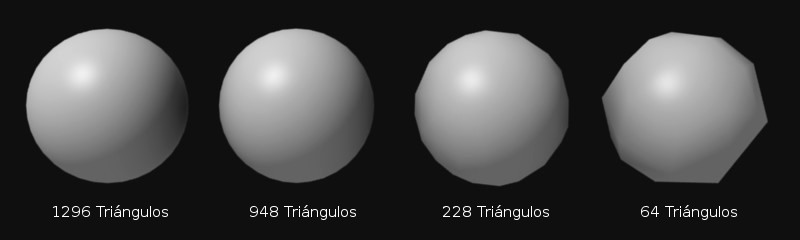 Figura 04. Variación del número de triángulos en una esfera. Esquema de suavizado. Autosuavizado Figura 05. Autosuavizado en un cilindro. En la mayoría de programas de diseño (entre ellos Blender), existe una opción de autosuavizado (Autosmooth). Esta opción suaviza selectivamente las caras que forman superficies sin aristas. Esta opción lleva siempre un argumento, el ángulo máximo tolerado. Todas las caras que formen entre si un ángulo menor que el indicado serán suavizadas mientras que el resto de las aristas serán consideradas como "duras", con bordes afilados. Ésto es muy útil y, de hecho, resulta imprescindible para representar superficies que combinan suavidad con cortes duros. Un buen ejemplo es el cilindro. Mientras que el cuerpo del cilindro es una superficie suave, sus tapas son como cortes a cuchillo de un supuesto cilindro infinito. Por lo tanto las tapas no han de ser suavizadas con el resto del cuerpo, sino que deben de considerarse superficies planas a parte. Las caras de las tapas forman un ángulo de 90 grados con las del cuerpo, de modo que basta con poner un ángulo de autosmooth inferior para conseguir el resultado deseado. En la Figura 05 se ve la diferencia entre el suavizado normal y el autosuavizado. Nótese como la tapa del cilindro se fusiona con el resto si usamos un suavizado normal.
Uso de TextoBlender tiene un buen soporte de opciones para trabajar con texto. ¡Incluso existe un fork del proyecto (  Figura 07. Opciones de Texto. Los elementos de texto son tratados internamente como un tipo de curvas, por lo que las opciones permitidas para estos objetos son similares a las que veremos en el trabajo con superficies curvas en la siguiente sección. Para añadir un texto lo haremos desde el menú principal Barra Espaciadora Add/ Text. Esto nos añadirá un texto Text en la ventana 3D, que podremos editar en Modo de Edición
Las opciones de la caja inferior permiten definir la apariencia del texto; tamaño, distancia entre líneas de texto (conocido en aplicaciones de maquetación como leading), distancia entre palabras, etc. En la pestaña Char (por defecto aparece situada detrás de la pestaña descrita anteriormente Font cuando el texto está en Modo de Edición) podemos acceder a caracteres concretos de esa fuente. Esto es especialmente interesante si usamos alguna tipografía con dibujos, iconos, etc... Definición de Marcos de Texto F 08. Marcos Blender sorprende con esta funcionalidad poco habitual en herramientas de diseño 3D, la definición de Marcos de Texto. Los marcos que pertenecen al mismo texto permiten que el texto que no quepa en el primero continue en el segundo, del segundo al tercero, y así sucevisamente (como se puede ver en el Player
Texto que sigue un caminoUn efecto interesante que permite Blender es situar un texto a lo largo de una curva. Para ello, se emplea el campo TextOnCurve de la pestaña Font vista anteriormente. En este campo se debe indicar el nombre de la curva que se quiere emplear como camino. 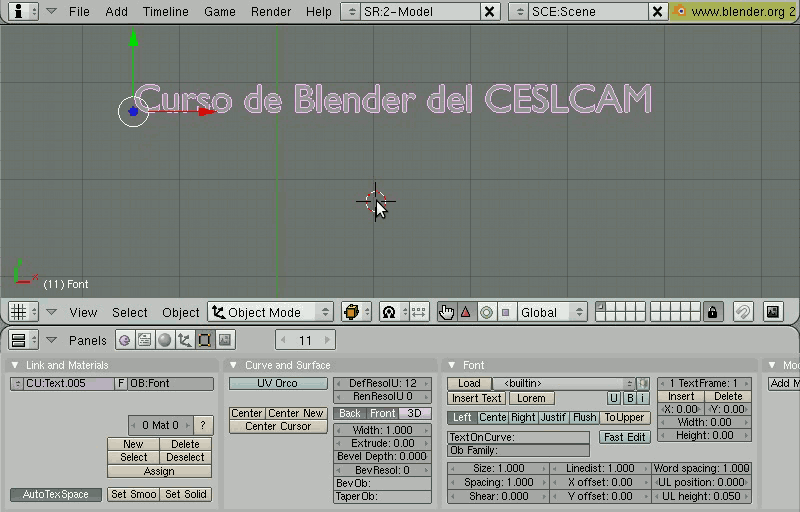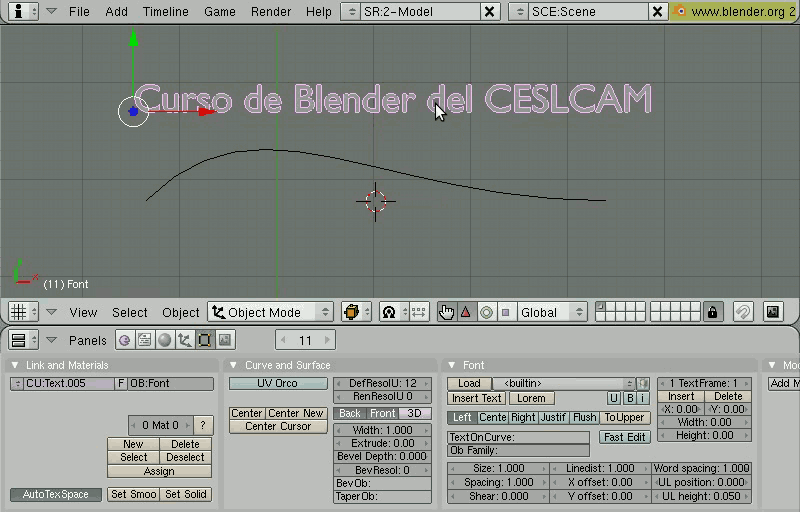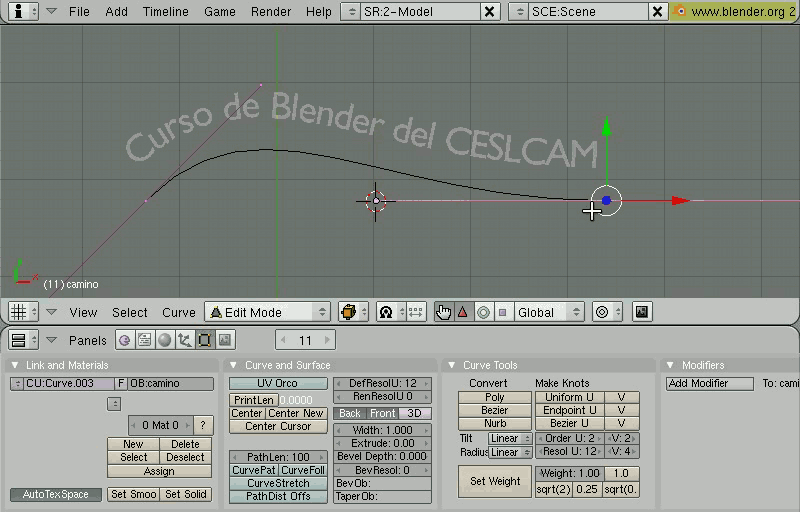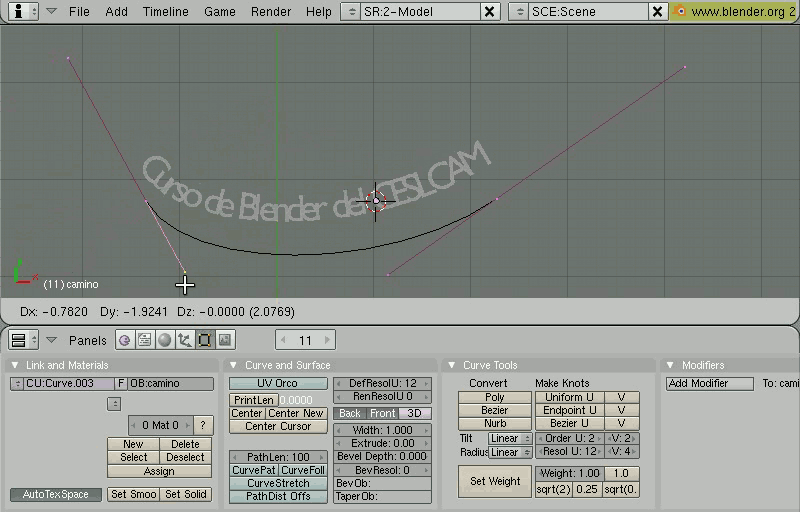 Figura 09. Configuración de texto que sigue un camino (curva de Bezier). Por ejemplo, podemos añadir una curva de Bézier Barra Espaciadora Add/ Curve/ Bézier Curve que servirá como camino. En modo de edición ajustaremos los puntos de control y cambiaremos el nombre del objeto en el campo OB: de la pestaña Link and Materials de los botones de edición Conversión de curva a malla poligonalHay muchos casos en los que interesa convertir un objeto curvo a malla poligonal (esta operación se denomina Teselación Tessellation), por ejemplo para convertir un texto 3D a un objeto que quieres distribuir sin tener que dar la fuente, en el caso de querer utilizar un objeto en el módulo de simulaciones físicas (fluidos, partículas), si quieres animar los objetos mediante un esqueleto... La conversión se realiza con el objeto curvo seleccionado en Modo de Objeto, pulsando Alt C Convert curve to mesh. El proceso inverso de conversión de malla poligional a superficie curva es algoritmicamente muy complicado de realizar con precisión. Blender, como la mayoría de aplicaciones 3D, no incorpora ninguna opción para realizar eta operación.
|
con el objeto en cuestión seleccionado.
Entonces nos aparecerá en la pestaña 
DTP Blender
. En los botones de edición 
nos permite empaquetar la fuente en el propio fichero .blend. Esto es útil si quieremos compartir el fichero y asegurarnos que pueden visualizar las fuentes correctamente. En general, siempre que aparece este icono, nos permite empaquetar el elemento relacionado para que vaya comprimido dentro del propio fichero .blend.
Video: 1:20